前言
本文主要参考 龙书三、用Go语言自制编译器 以及网课:湖南大学2024计科拔尖班-《编译原理》
大部分知识点会附上图例以及真实可用的代码(本文所有图片与代码均为作者原创)代码部分主要使用 python
另有一点要注意:
本文所提到的 “DFA” 并非严谨定义的 “确定性有穷自动机”,为了简化概念,本文直接省略了“死状态”及其相关的弧
词法分析器简介
什么是词法分析器?它是绝大部分编译器的入口模块,它负责将源代码分割成为一个个词法单元
将其作为黑盒看待:其输入为源代码或者字节流,输出为标记流(Token Stream)
举个例子,对于源代码:
if (i == j):
z = 1;
else:
z = 2;
一种可能的分割为:
[keyword 'if'] [left_bracket '('] [id 'i'] [double_equal '=='] [id 'j'] [right_bracket ')'] [colon ':']
[id 'z'] [equal '='] [number '1'] [semicolon ';']
[keyword 'else'] [colon ':']
[id 'z'] [equal '='] [number '2'] [semicolon ';']
通过这个例子可以窥见一些词法分析的思想和意义,我们将源代码中的“关键字”、“标识符” 等元素分离成独立的 Token,并且将空白符等与程序逻辑无关的内容丢弃(这里不太严谨,部分编程语言中空白符是有语法意义的,例如 python),这些信息和原始代码相比更加结构化,便于后续的处理
关于词法单元
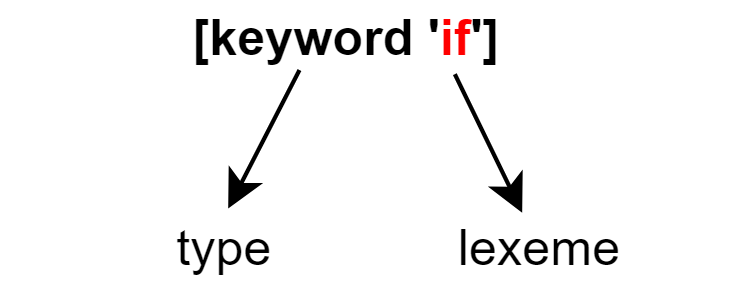
一个词法单元拥有两个属性,一个是词法单元的类型 type,另一个是词素 lexeme
type 用于标识该词法单元的类别,lexeme 则用于补充一些额外信息
以 [keyword 'if'] 为例,其类型为 keyword,标识了该词法单元是一个关键字;词素中记录了该词法单元的字面量 'if',指出了其具体命中的关键字是 if 而不是 else 等其他关键字
词素不仅可以记录字面量,通常还会记录该词法单元对应字面量在源代码中的行列号,这样在出现解析错误等问题时可以指示出发生错误的具体位置
手工构造的词法分析器
能手动控制解析过程;意味着可以对各个部分的细节进行相当好的控制,效率高
相对复杂且容易出错,但是是目前非常流行的实现方法
这是一种朴素的词法分析思路,可以总结为:构造并使用“转移图”来做词法分析
例如,当我们有如下词法分析任务时:
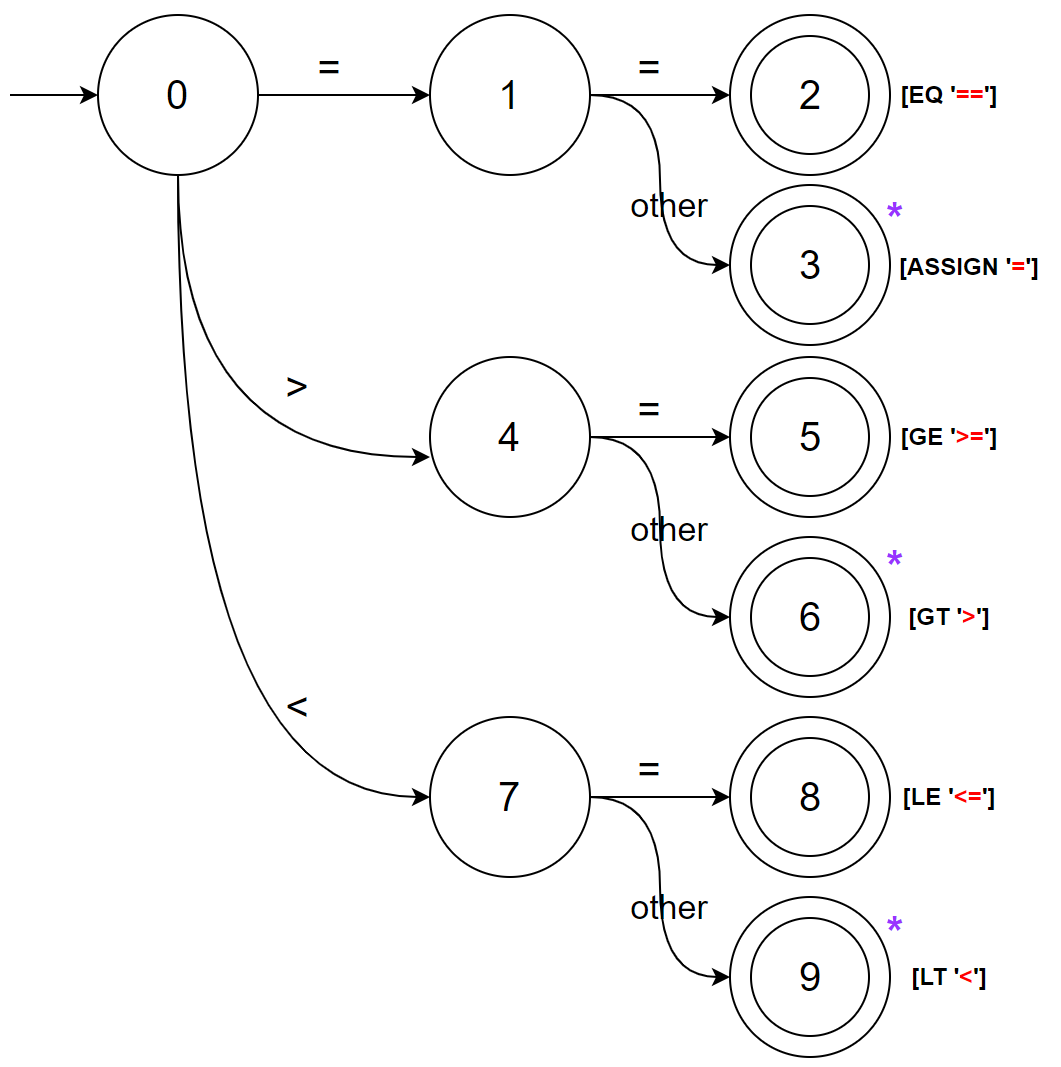
区分词法单元 = > < >= <= ==
则可以构造如下转移图
转移图包含了两种元素:状态和弧,其中中间带数字标号的圆圈即为“状态”,连接各个状态的有指向性的连线即为“弧”
“状态”又分为了:起始状态、普通状态、终止状态;上图中的状态 0 为起始状态,用一条没有出发节点的弧标识;状态 2,3,5,6,8,9 为终止状态,用双层圆圈来标识
“弧”表达了某个状态的“转移条件”,当读入的字符满足转移条件时,将会沿着对应的边进行状态转移;例如当我们处于状态 0 时,读入一个字符,当读入的字符为 = 时,将会转移到状态 1
到达了终止状态即表示命中了某个词法单元,将会结束该转移图并输出对应的 Token,例如到达状态 2 时将会输出 Token [EQ '==']
有些终止状态的右上角会有星标,这表示“回溯”,例如到达状态 3 时,将会输出 Token [ASSIGN '='],然后结束转移图,然后将输入回退一个位置(即回退到读入”other”之前)
用伪代码来表示上述转移图,就是:
nextToken():
eat a char
match currentChar
case '=':
eat a char
match currentChar:
case '=': return EQ
case other: rollback and return ASSIGN
case '>':
eat a char
match currentChar
case '=': return GE
case other: rollback and return GT
case '<':
eat a char
match currentChar:
case '=': return LE
case other: rollback and return LT
case other:
return error
用 python 实现该逻辑:
定义 Token 的数据结构
class Token():
def __init__(self, token_type: str, lexeme: str) -> None:
self.type: str = token_type
self.lexeme: str = lexeme
def __str__(self) -> str:
return f"[{self.type} '{self.lexeme}']"
按照转移图实现词法分析器
class Lexer():
def __init__(self, input_: str) -> None:
self.input: str = input_
self.ptr: int = -1
self.current_char: str = ''
def move_ptr(self) -> None:
self.ptr += 1
if self.ptr >= len(self.input):
self.current_char = ''
else:
self.current_char = self.input[self.ptr]
def rollback_ptr(self) -> None:
self.ptr = max(0, self.ptr-1)
self.current_char = self.input[self.ptr]
def next_token(self) -> Token:
self.move_ptr()
if not self.current_char:
return Token('EOF', '')
token: Token = Token('ILLEGAL', '')
match self.current_char:
case '=':
self.move_ptr()
if self.current_char == '=':
token = Token('EQ', '==')
else:
self.rollback_ptr()
token = Token('ASSIGN', '=')
# 与上述代码类似, 略
case '>':...
case '<':...
case _:
token = Token('ILLEGAL', self.current_char)
return token
调用 Lexer 进行词法分析
src = input("please enter your code: ")
lexer = Lexer(input_=src)
while True:
token = lexer.next_token()
if token.type == 'EOF':
break
print(token, end=" ")
print("")
我们还可以加入对空白符的识别,并且在输出时忽略空白符
case ' ' | '\n' | '\r' | '\t':
literal = self.current_char
while True:
self.move_ptr()
if not self.current_char.isspace():
self.rollback_ptr()
break
literal += self.current_char
token = Token('WHITESPACE', literal)
src = input("please enter your code: ")
lexer = Lexer(input_=src)
while True:
...
if token.type == 'WHITESPACE':
continue
...
对于更加复杂的词法分析要求,我们只需要扩充转移图,然后根据转移图手工构造等效的解析代码即可
一个功能完善的编程语言很可能需要非常庞大的转移图来描述其词法分析过程,这就导致手工构造的词法分析器”相对复杂且容易出错“
下面是一些技巧补充
利用前看字符消除回溯
对于转移图
eat a char
match current_char:
case '=':
eat a char
match current_char:
case '=': return EQ
case other: rollback and return ASSIGN
我们可以改写成
eat a char
match current_char:
case '=':
match peek_char:
case '=': eat a char and return EQ
case other: return ASSIGN
这里的 peek_char 就是前看字符,我们通过窥视下一个即将读入的字符,来判断转移图的走向,从而消除了回溯
用这种方法还能很好地减少代码量,因为转移图的大部分分支会像这样:
eat a char
match current_char:
case 'a': return A
...
如果不使用 peek_char,则会变成:
eat a char
match current_char:
case 'a':
eat a char
match current_char:
case other: rollback and return A
...
不仅代码量更多,而且多执行了一次 eat a char 和 rollback,导致更多开销
使用该技巧改写上面的 Lexer:
class Lexer():
def __init__(self, input_: str) -> None:
self.input: str = input_
self.frontptr: int = -1
self.backptr: int = 0
self.current_char: str = ''
self.peek_char: str = ''
def move_ptr(self) -> None:
self.frontptr += 1
self.backptr += 1
self.current_char = (
self.input[self.frontptr] if self.frontptr < len(self.input) else '')
self.peek_char = (
self.input[self.backptr] if self.backptr < len(self.input) else '')
def next_token(self) -> Token:
self.move_ptr()
if not self.current_char:
return Token('EOF', '')
token: Token = Token('ILLEGAL', '')
match self.current_char:
case '=':
if peek_char == '=':
self.move_ptr()
token = Token('EQ', '==')
else:
token = Token('ASSIGN', '=')
# 与上述代码类似, 略
case '>':...
case '<':...
case _:
token = Token('ILLEGAL', self.current_char)
return token
利用关键字表简化关键字识别
当关键字较多时,如果还将关键字的解析逻辑表现在转移图上,则会使转移图十分臃肿且难以阅读
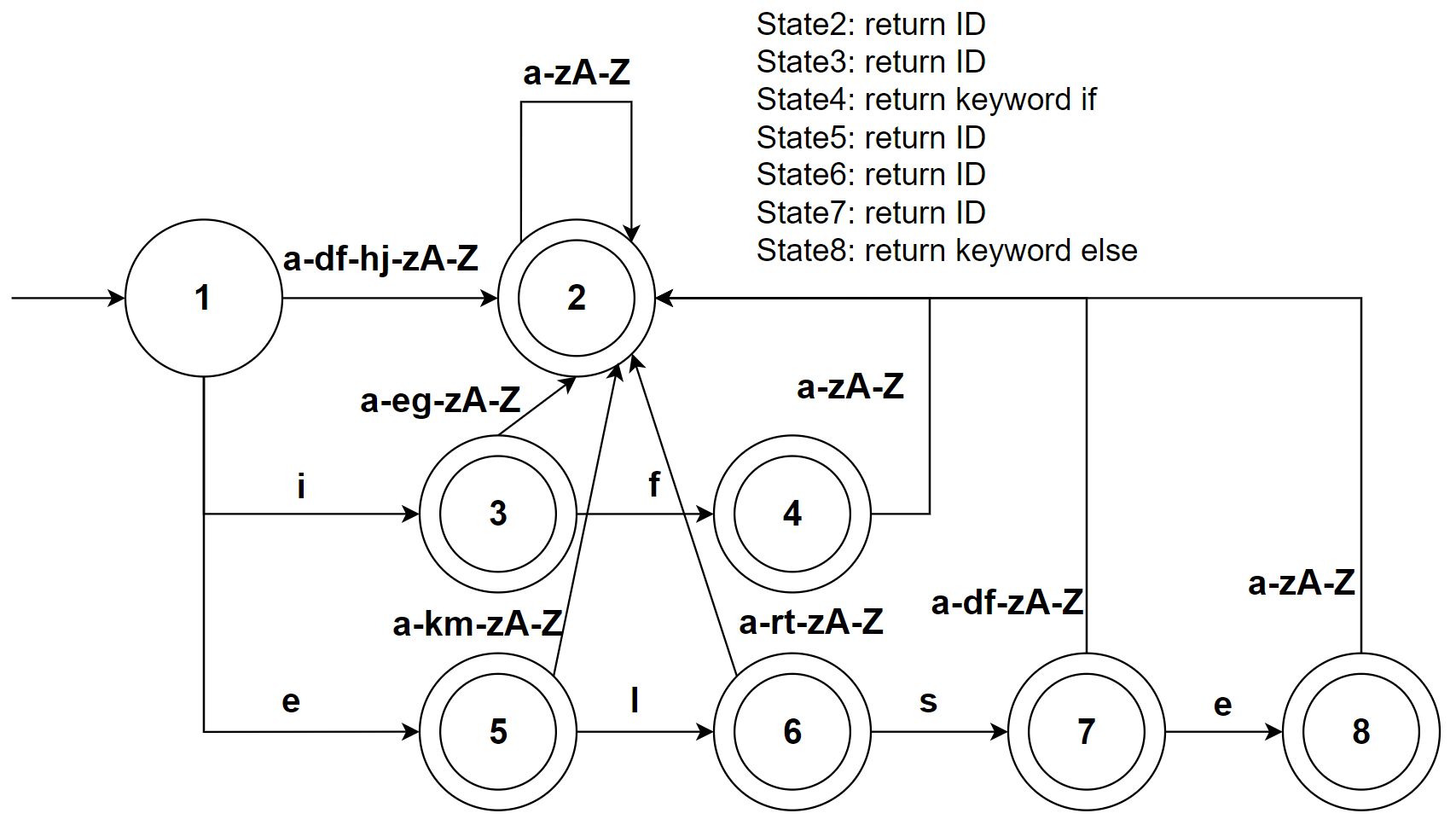
例如:解析关键字 if else,以及由大小写字母组成的标识符
那么有转移图:
可以看到即使只有两个关键字,我们构造的转移图就十分臃肿了
这是因为在大部分编程语言中,关键字的词法规则(在上面的例子是中是 if|else)经常成为为标识符的词法规则(在上面的例子中是 a-zA-Z)的子集,为了区分关键字和标识符,我们不得不做好准备:随时从关键字集合转移到标识符集合
幸运的是,我们能够使用“关键字表”的技巧来简化这个任务;既然关键字是标识符的子集,我们完全可以将其作为标识符来处理,然后将匹配到的标识符与关键字表对比,如果在关键字表中,说明该词法单元是关键字,否则是标识符
以下是伪代码
isLetter(char):
return Ture if char in a-zA-Z
else return Flase
keywords: [ "if", "else" ]
nextToken():
eat a char
match current_char:
case isLetter(current_char):
eat char while isLetter(peek_char)
if the word in keywords: return KEYWORD[word]
else: return ID[word]
case other:
return error
python 代码实现:
class Token():...
keywords: dict[str, str] = {
"if": "IF", "else": "ELSE"
}
def is_letter(ch: str) -> bool:
return (
('a' <= ch and ch <= 'z')
or ('A' <= ch and ch <= 'Z'))
class Lexer():
def __init__(self, input_: str) -> None:...
def move_ptr(self) -> None:...
def next_token(self) -> Token:
self.move_ptr()
if not self.current_char:
return Token('EOF', '')
match self.current_char:
case _:
if is_letter(self.current_char):
literal = self.current_char
while is_letter(self.peek_char):
literal += self.peek_char
self.move_ptr()
token = Token(keywords.get(literal, 'ID'), literal)
elif self.current_char.isspace():
literal = self.current_char
while self.peek_char.isspace():
literal += self.peek_char
self.move_ptr()
token = Token('WHITESPACE', literal)
else:
token = Token('ILLEGAL', self.current_char)
return token
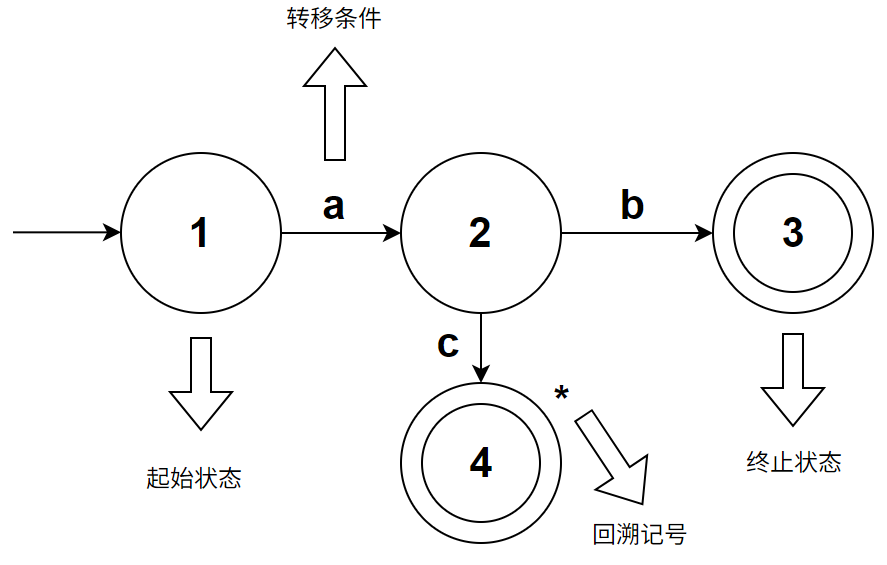
代码表示转移图的另一种写法
该方法使用两层 match case 来表示转移图,具体思路是:外层 case 覆盖转移图的所有状态,内层 case 覆盖对应状态的所有转移条件
例如,对于转移图
伪代码如下:
nextToken():
state = 0
while True:
match state:
case 0:
eat a char
match current_char:
case '=': state = 1
case '>': state = 4
case '<': state = 7
default: return ERROR
case 1:
eat a char
match current_char:
case '=': state = 2
default: state = 3
case 2:
return EQ
case 3:
rollback and return ASSIGN
case 4: ...
case 5: ...
case 6: ...
case 7: ...
case 8: ...
case 9: ...
该方法能够很方便地表示一些结构十分复杂的转移图
词法分析器生成工具
代码量少、开发速度快,但是较难把控细节
高校考试喜欢考 🤣
这种方法使用正则表达式描述词法规则,通过输入的规则,自动生成词法分析算法
我们有许多成熟的工具可用,例如:Lex、Flex、Ply、Lark、Antlr …
但是本文不是教学如何使用这些现有工具的,而是探索这类工具的原理
正则表达式
不含任何语法糖的 regex 包含:
- ε:空字符
- c ∈ ∑:单字符
- R1 R2:先匹配 R1 然后匹配 R2
- R1|R2:匹配 R1 或者 R2
- R*:称作e的闭包,可以表示为 (ε | R | RR | RRR | …)
现代语言中的支持的正则表达式往往会引入一些语法糖,例如
- R?:0个或1个R,可以使用 ε | R 来构建
- R+:1个或多个R,可以使用 R R* 来构建
- [c1-cn]:可以表示为 c1 | c2 | … | cn
语法糖不是必须的,本文涉及到 regex 的部分将不讨论语法糖,仅考虑最原始的 5 条规则
将上述规则总结为文法,则能获得 regular expression 的数学定义:
% LaTeX
\begin{align}
R &\rightarrow \epsilon\\
&\quad |\ c \in \Sigma\\
&\quad |\ RR\\
&\quad |\ R|R\\
&\quad |\ R^*\\
\end{align}
NFA 和 DFA
NFA 指的是“非确定有限自动机”(non-determinisic finite automata),DFA 指的是“确定有限自动机”(determinisic finite automata)
以下内容节选自龙书三
NFA 可以视作一个五元组 (S, ∑, M, s0, F)
- 一个有穷的状态集合 S
- 一个输入符号集合 ∑(这里假设 ε 不是 ∑ 中的元素)
- 一个转换函数 M,它为每个状态和 ∑ ∪ {ε} 中的每个符号都给出了相应的后续状态的集合
- s0 ∈ S,为开始状态
- F ⊆ S,为终止状态的集合
DFA 是 NFA 的一种特殊情况,其中:
- 没有输入 ε 之上的转换动作
- 对于每个状态 s 和每个符号 a,有且仅有一条标号为 a 的边离开 s
龙书用离散数学的语言描述了 NFA 和 DFA 的定义,稍微有点晦涩。我们也可以借助前面提到的”转移图“来理解 NFA 和 DFA
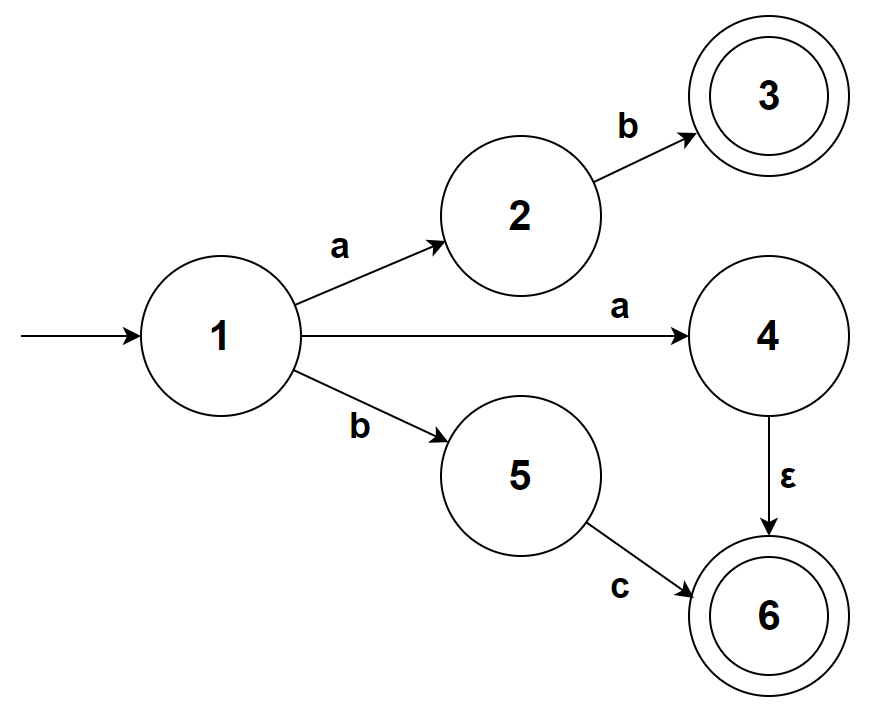
下面是一个合法的 NFA:
该 NFA 的 S 为 {1,2,3,4,5,6};∑ 为 {a,b,c,ε};s0 为 1,F 为 {3,6}
M 则可以表示为下面的表格
| 状态\符号 | a | b | c | ε |
|---|---|---|---|---|
| 1 | {2,4} | {5} | ∅ | ∅ |
| 2 | ∅ | {3} | ∅ | ∅ |
| 3 | ∅ | ∅ | ∅ | ∅ |
| 4 | ∅ | ∅ | ∅ | {6} |
| 5 | ∅ | ∅ | {6} | ∅ |
| 6 | ∅ | ∅ | ∅ | ∅ |
可以看到对于状态1,有两条符号为 a 的边,对于状态4,有一条符号为 ε 的边(这些都是 DFA 不允许的)
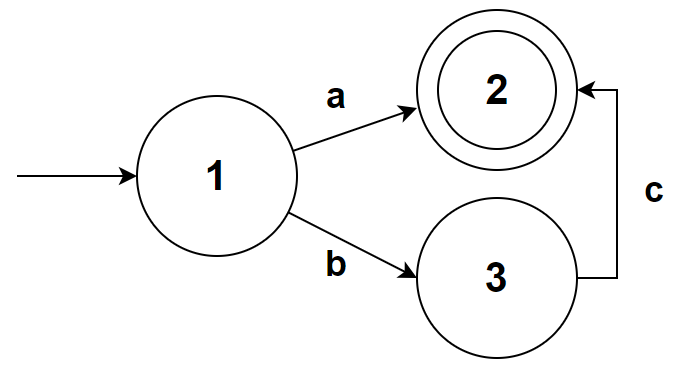
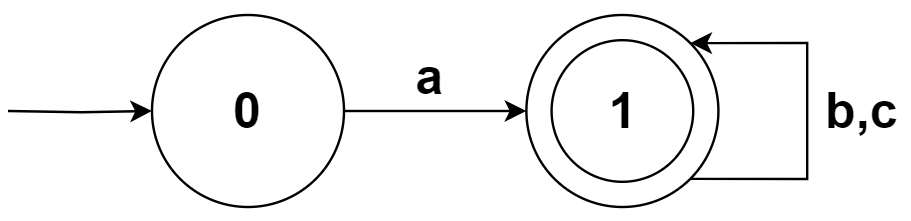
下面是一个合法的 DFA(省略了死状态):
可以看到 DFA 没有符号为 ε 的边,对于每个状态 s,都仅有一条标号 c∈∑ 的边离开 s
也就是说 M 表格中的元素不再需要用集合来表示,而是一个确定的状态标号
| 状态\符号 | a | b | c |
|---|---|---|---|
| 1 | 2 | 3 | ∅ |
| 2 | ∅ | ∅ | ∅ |
| 3 | ∅ | ∅ | 2 |
有没有发现 DFA 的转移图和”手工构造的词法分析“使用的转移图在结构上一致;这意味着,只要我们有办法”自动地”生成一个 DFA,就能构建出像 Lex 和 Flex 那样的词法分析工具
怎么“自动地”生成一个用于分析特定词法规则的 DFA 呢?下面介绍几种算法来解决这个问题
Thopsom 构造法: RE -> NFA
该算法由图灵奖得主 Kenneth Lane Thopsom 发明,是一个基于“简单规则直接构造,复杂规则递归构造”的将正则表达式转换为等价 NFA 的算法
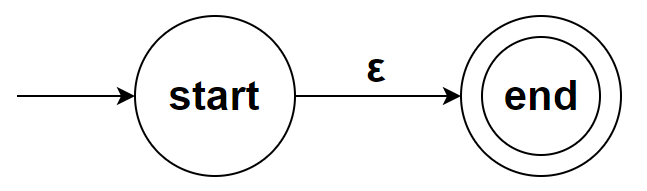
对于简单的规则:ε 和 c∈∑,我们直接构造
ε
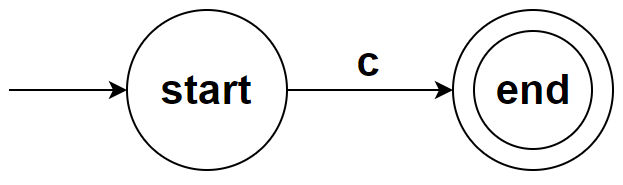
c∈∑
注意到直接构造的 NFA 均只有一个结束条件
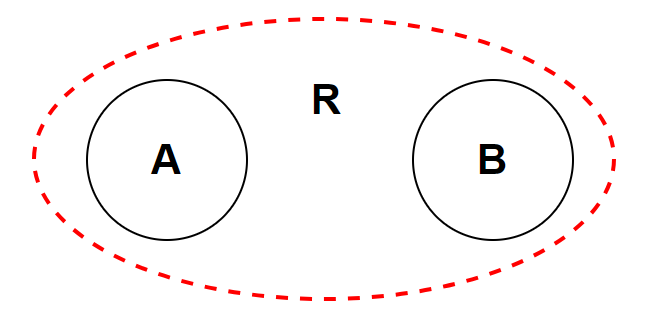
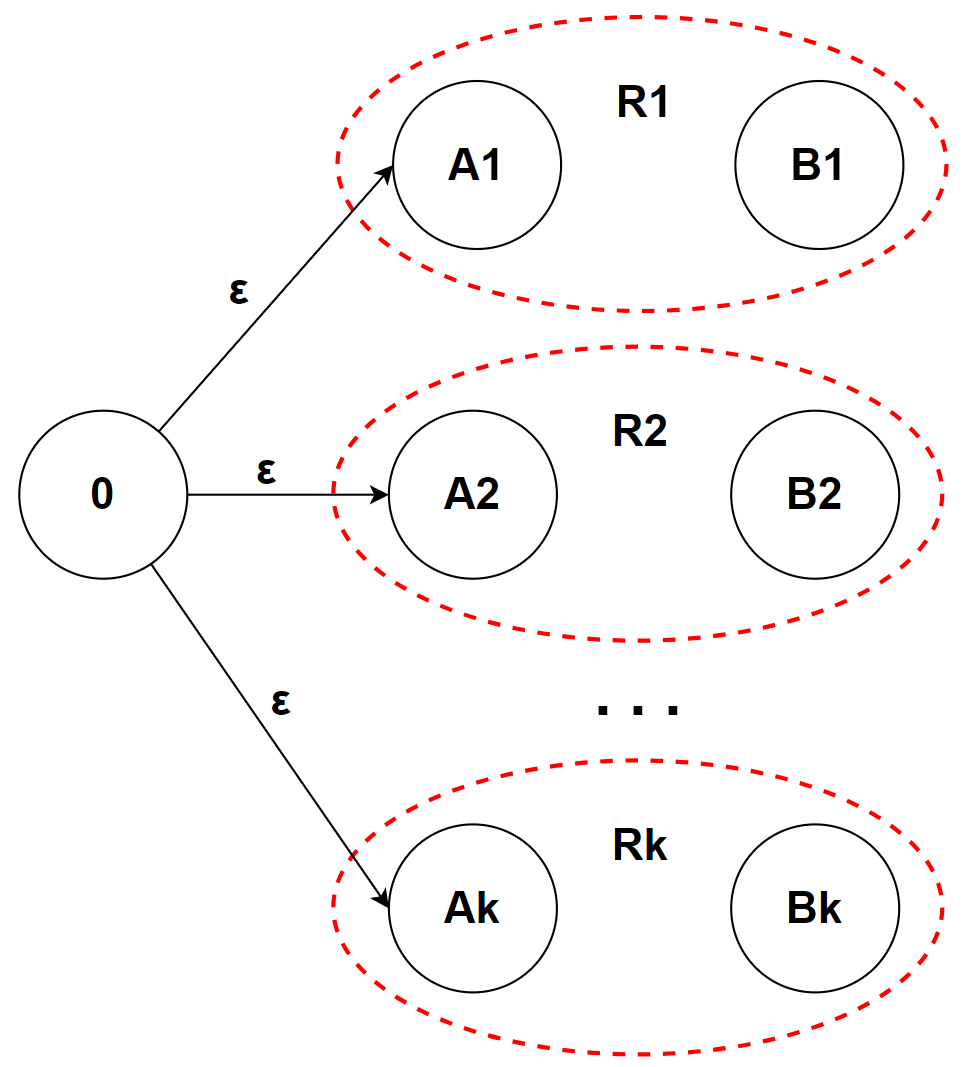
于是我们假设构造出的 NFA 均只有一个结束条件,则可以将任意一个 regex 的等效 NFA 抽象成下面的形式:
其中 R 为该正则表达式的规则,A 为起始状态,B 为终止状态
基于这个假设,我们可以递归构造出复杂规则的 NFA
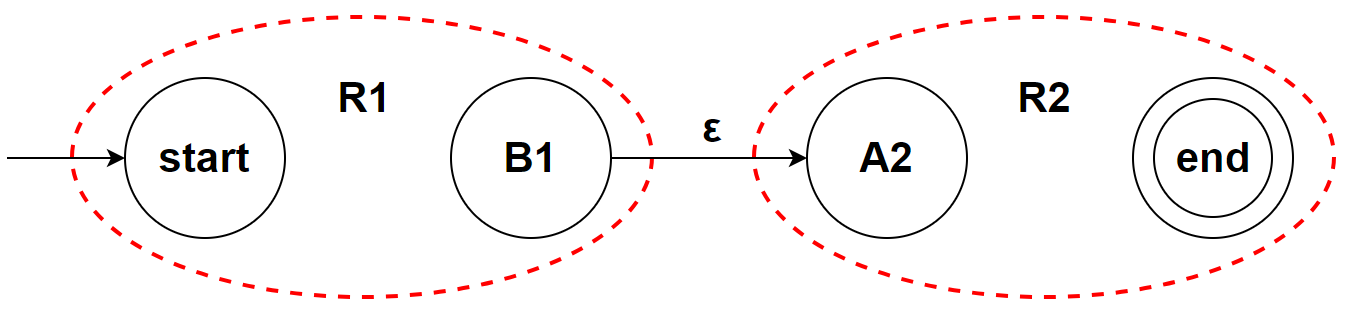
R1 R2
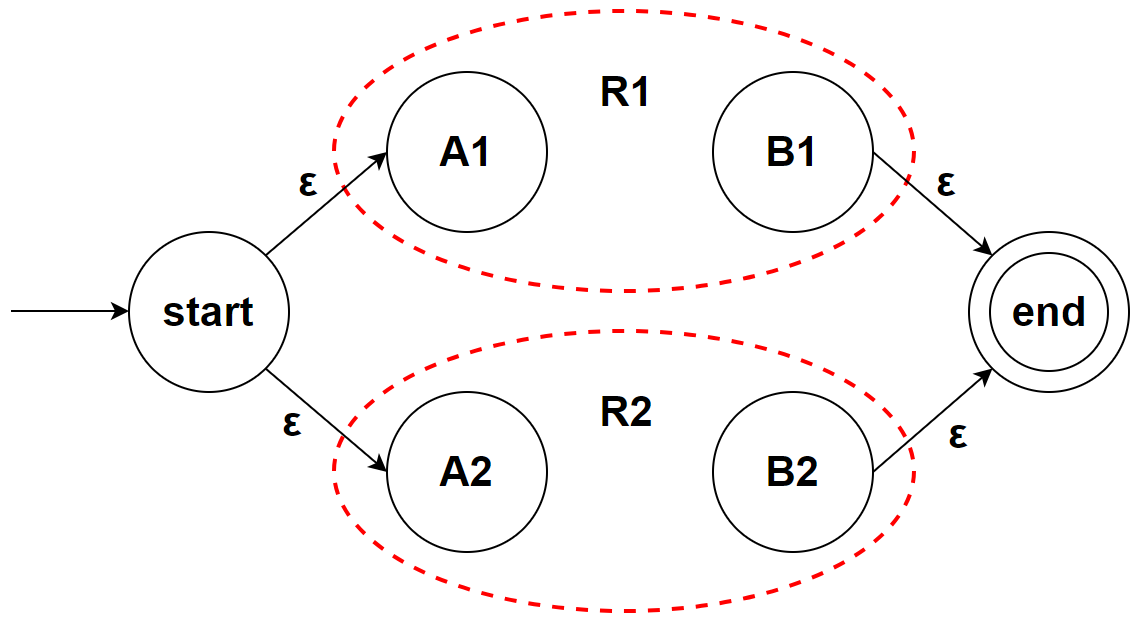
R1|R2
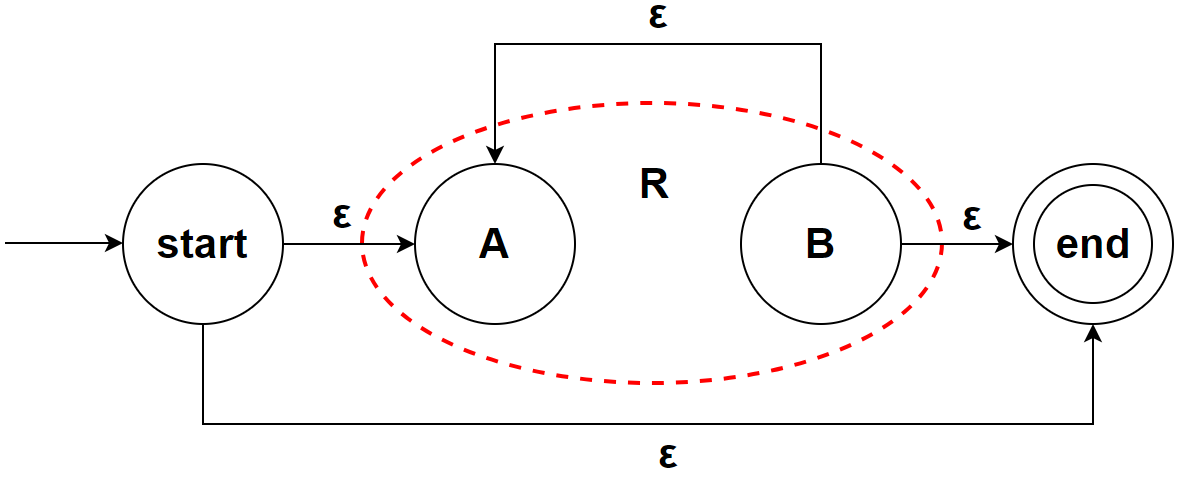
R*
至此我们完成了构造方法的归纳,符合假设,证明了该方法的正确性
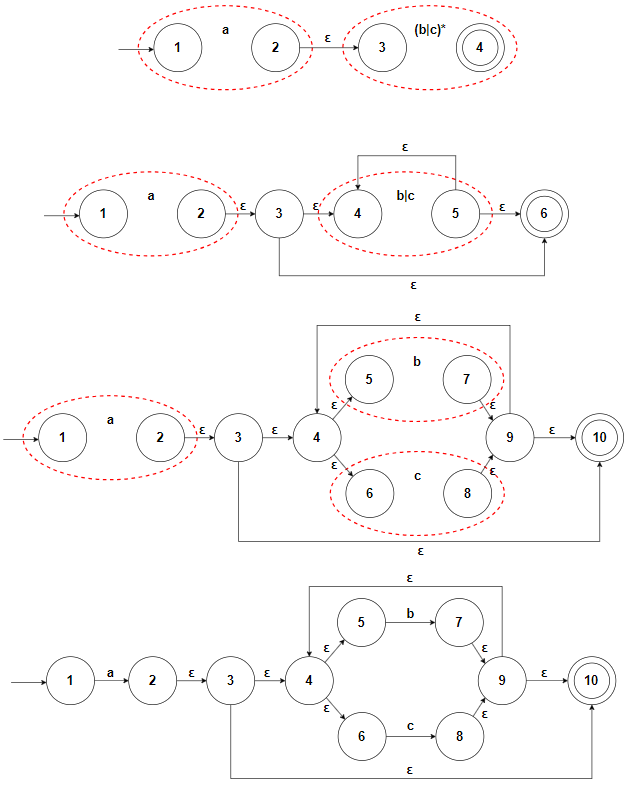
尝试使用该算法构造 a(b|c)* 的 NFA:
下面是 Thopsom 算法的 python 实现,对于最原始的正则表达式,我们可以将其转化为后缀表达式来解析(如果你想,甚至可以用 Pratt 解析的方式来完成这个任务,这样能更好地扩展正则表达式支持的语法,不过这是语法分析的内容了)
首先定义 NFA 的数据结构
class NFA():
def __init__(self):
self.states: set[int] = set()
self.s0: int = None
self.final: set[int] = set()
self.conditions: set[str] = set()
self.trans_table: dict[int, dict[str, set[int]]] = {}
def __repr__(self) -> str:
return f"S: {self.states}\n∑: {self.conditions}\nM: {self.trans_table}\ns0: {self.s0}\nF: {self.final}"
def new_state(self) -> int:
S: int = len(self.states)
self.states.add(S)
self.trans_table[S] = {}
return S
def link(self, S1: int, S2: int, condition: str) -> None:
if S1 not in self.states or S2 not in self.states:
raise KeyError("no such state")
self.conditions.add(condition)
if not self.trans_table[S1].get(condition):
self.trans_table[S1][condition] = set()
self.trans_table[S1][condition].add(S2)
然后添加 Thopsom 构造法的构造规则(可以结合前面的图像来理解代码)
type StateA = int
type StateB = int
type SubNFA = tuple[StateA, StateB]
EPSILON: str = "<epsilon>"
class NFA():
def __init__(self):...
def __repr__(self) -> str:...
def new_state(self) -> int:...
def link(self, S1: int, S2: int, condition: str) -> None:...
def new_epsilon(self) -> SubNFA:
"ε"
# 创建状态
A: StateA = self.new_state()
B: StateB = self.new_state()
# 创建边
self.link(A, B, EPSILON)
# 更新起始状态
if not self.s0: self.s0 = A
# 更新结束状态
self.final.add(B)
return (A, B)
def new_char(self, char: str) -> SubNFA:
"c∈∑"
if len(char) > 1:
raise ValueError("char too long")
# 创建状态
A: StateA = self.new_state()
B: StateB = self.new_state()
# 创建边
self.link(A, B, char)
# 更新起始状态
if not self.s0: self.s0 = A
# 更新结束状态
self.final.add(B)
return (A, B)
def concat(self, R1: SubNFA, R2: SubNFA) -> SubNFA:
"R1 R2"
# 创建状态
A1, B1 = R1
A2, B2 = R2
# 创建边
self.link(B1, A2, EPSILON)
# 更新起始状态
if self.s0 == A2: self.s0 = A1
# 更新结束状态
self.final.remove(B1)
return (A1, B2)
def union(self, R1: SubNFA, R2: SubNFA) -> SubNFA:
"R1 | R2"
# 创建状态
A1, B1 = R1
A2, B2 = R2
S: StateA = self.new_state()
E: StateB = self.new_state()
# 创建边
self.link(S, A1, EPSILON); self.link(S, A2, EPSILON)
self.link(B1, E, EPSILON); self.link(B2, E, EPSILON)
# 更新起始状态
if self.s0 == A1: self.s0 = S
if self.s0 == A2: self.s0 = S
# 更新结束状态
self.final.remove(B1)
self.final.remove(B2)
self.final.add(E)
return (S, E)
def closure(self, R: SubNFA) -> SubNFA:
"R*"
# 创建状态
A, B = R
S: StateA = self.new_state()
E: StateB = self.new_state()
# 创建边
self.link(S, A, EPSILON); self.link(S, E, EPSILON)
self.link(B, A, EPSILON); self.link(B, E, EPSILON)
# 更新起始状态
if self.s0 == A: self.s0 = S
# 更新结束状态
self.final.remove(B)
self.final.add(E)
return (S, E)
最后将输入的正则表达式转化为后缀表达式形式,用其构建 NFA
一般使用 Shunting-yard 算法完成“中缀表达式转后缀表达式”的任务,该部分不属于编译原理的内容
高校大概会有一门叫《数据结构》的课讲这个,本文不会介绍此算法
在这个场景下有需要注意的点,那就是像 R1 R2 这样的 “连接”运算是没有显式运算符的,所以我们要通过预处理来显式地增加连接运算符
from enum import StrEnum
# 定义正则表达式的运算符
class ReOperator(StrEnum):
CONCAT = '<concat>'
UNION = '|'
CLOSURE = '*'
LBRACKET = '('
RBRACKET = ')'
class Regex():
# 运算符优先级表
OperatorLevel: dict[str, int] = {
ReOperator.CLOSURE: 4,
ReOperator.LBRACKET: 3,
ReOperator.CONCAT: 2,
ReOperator.UNION: 1,
}
def __init__(self, pattern: str) -> None:
self.pattern: str = pattern
def pretreatment(self, pattern: str) -> list[str]:
"预处理, 显式增加 concat 运算符"
result = []
for i in range(len(pattern)):
char = pattern[i]
result.append(char)
if char not in ReOperator or char == ReOperator.RBRACKET or char == ReOperator.CLOSURE:
if i+1 >= len(pattern):
continue
peek = pattern[i+1]
if peek not in ReOperator or peek == ReOperator.LBRACKET:
result.append(ReOperator.CONCAT)
return result
def oplevel(self, char) -> int:
return self.OperatorLevel.get(char, -1)
def to_suffix(self) -> list[str]:
"获取正则表达式的后缀表达式形式"
result: list[str] = []
stack: list[str] = []
for char in self.pretreatment(self.pattern):
match char:
case ReOperator.UNION | ReOperator.CLOSURE | ReOperator.CONCAT:
while len(stack):
o = stack[-1]
if (self.oplevel(o) < self.oplevel(char)
or o == ReOperator.LBRACKET):
break
result.append(stack.pop())
stack.append(char)
case ReOperator.LBRACKET:
stack.append(char)
case ReOperator.RBRACKET:
while len(stack):
o = stack.pop()
if o == ReOperator.LBRACKET:
break
result.append(o)
case _:
result.append('' if char == 'ε' else char)
while len(stack):
result.append(stack.pop())
return result
def to_nfa(self) -> NFA:
"通过后缀表达式建立 NFA"
nfa: NFA = NFA()
stack: list[SubNFA] = []
for i in self.to_suffix():
match i:
case ReOperator.CONCAT:
R2 = stack.pop()
R1 = stack.pop()
stack.append(nfa.concat(R1, R2))
case ReOperator.UNION:
R2 = stack.pop()
R1 = stack.pop()
stack.append(nfa.union(R1, R2))
case ReOperator.CLOSURE:
R = stack.pop()
stack.append(nfa.closure(R))
case '':
stack.append(nfa.new_epsilon())
case _:
stack.append(nfa.new_char(i))
return nfa
test_regex: Regex = Regex("a(b|c)*")
test_nfa: NFA = test_regex.to_nfa()
print(test_nfa)
子集构造算法: NFA -> DFA
子集构造算法(subset construction)是将 NFA 转换为 DFA 的一种算法
其基本思想是让构造得到的 DFA 的每个状态对应于 NFA 的一个状态集合,这样 DFA 的某个状态 Sd 就能“并行地”模拟对应 NFA 状态集合 {Sni, Snj, Snk...} 在遇到一个给定输入时可能执行的所有动作;从而消除 NFA 的“不确定性”
该算法依赖几种在 NFA 上的操作:
| 操作 | 描述 |
|---|---|
| epsilon-closure(s) | 能够从 s ∈ S 开始,只通过 ε 转换到达的 NFA 状态集合 |
| epsilon-closure(T) | 能够从 T ⊆ S 中的某个状态 s 开始,只通过 ε 转换到达的 NFA 状态集合,即 $\cup_{s∈T} \epsilon-closure(s)$ |
| move(T, a) | 能够从 T ⊆ S 中的某个状态 s 出发通过标号为 a 的转换到达的 NFA 状态集合 |
子集构造算法的伪代码如下:
subset_construction(NFA):
create S, ∑, M, s0, F for DFA
∑ = NFA.∑ - epsilon
s0 = epsilon_closure(NFA.s0)
put s0 in S, and s0 is unmarked
while (T in S is unmarked):
mark T
foreach (char in ∑):
U = epsilon_closure(move(T, char))
if (U not in S): put U in S, and U is unmarked
M[T, char] = U
put all the states that include NFA.F to F
return (S, ∑, M, s0, F)
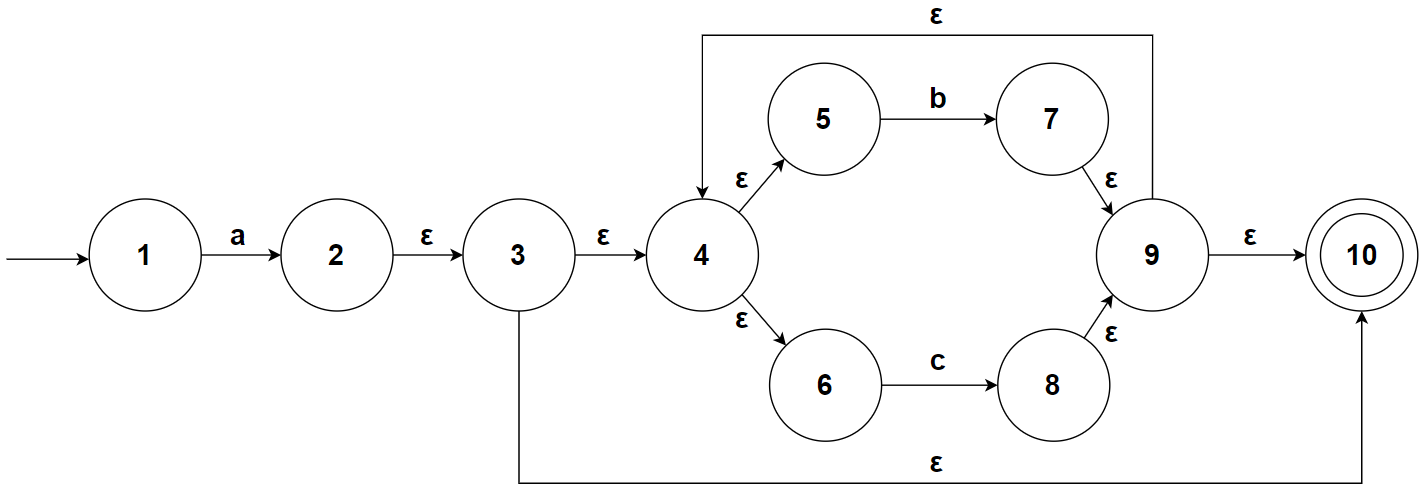
以前面构造的 a(b|c)* 的 NFA 为例
对于开始状态1,其 epsilon-closure(1) 为 {1}
于是有
| NFA-state | DFA-state | a | b | c |
|---|---|---|---|---|
| {1} | A |
对于状态 A:
epsilon_closure(move(A, a)) = epsilon_closure(2) = {2, 3, 4, 5, 6, 10}
epsilon_closure(move(A, b)) = epsilon_closure({}) = {}
epsilon_closure(move(A, c)) = epsilon_closure({}) = {}
于是有
| NFA-state | DFA-state | a | b | c |
|---|---|---|---|---|
| {1} | A | B | ∅ | ∅ |
| {2, 3, 4, 5, 6, 10} | B |
对于状态 B:
epsilon_closure(move(B, a)) = epsilon_closure({}) = {}
epsilon_closure(move(B, b)) = epsilon_closure(7) = {4, 5, 6, 7, 9, 10}
epsilon_closure(move(B, c)) = epsilon_closure(8) = {4, 5, 6, 8, 9, 10}
于是有
| NFA-state | DFA-state | a | b | c |
|---|---|---|---|---|
| {1} | A | B | ∅ | ∅ |
| {2, 3, 4, 5, 6, 10} | B | ∅ | C | D |
| {4, 5, 6, 7, 9, 10} | C | |||
| {4, 5, 6, 8, 9, 10} | D |
对于状态 C:
epsilon_closure(move(C, a)) = epsilon_closure({}) = {}
epsilon_closure(move(C, b)) = epsilon_closure(7) = {4, 5, 6, 7, 9, 10} (状态C)
epsilon_closure(move(C, c)) = epsilon_closure(8) = {4, 5, 6, 8, 9, 10} (状态D)
对于状态 D:
epsilon_closure(move(D, a)) = epsilon_closure({}) = {}
epsilon_closure(move(D, b)) = epsilon_closure(7) = {4, 5, 6, 7, 9, 10} (状态C)
epsilon_closure(move(D, c)) = epsilon_closure(8) = {4, 5, 6, 8, 9, 10} (状态D)
于是有
| NFA-state | DFA-state | a | b | c |
|---|---|---|---|---|
| {1} | A | B | ∅ | ∅ |
| {2, 3, 4, 5, 6, 10} | B | ∅ | C | D |
| {4, 5, 6, 7, 9, 10} | C | ∅ | C | D |
| {4, 5, 6, 8, 9, 10} | D | ∅ | C | D |
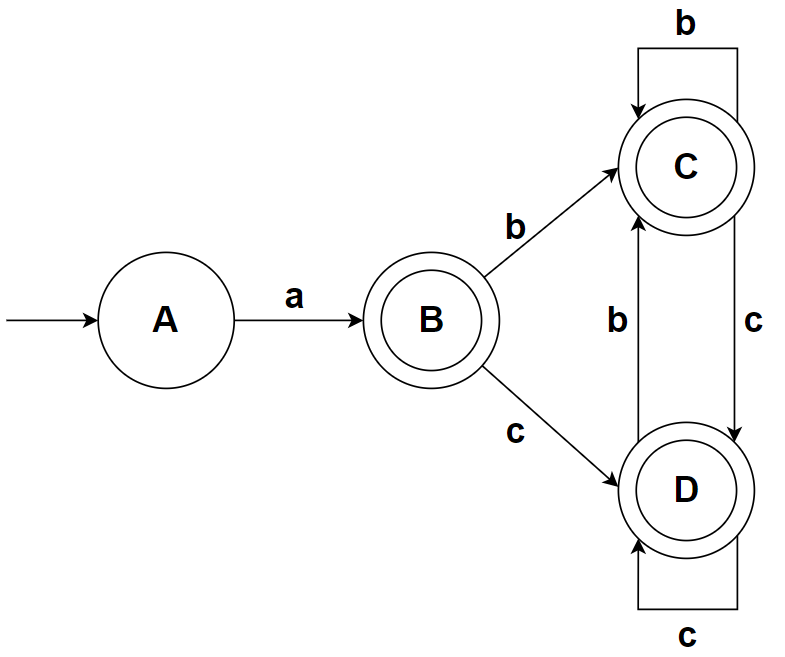
至此构造完毕,其中 A 为开始状态,因为 B、C、D 包含了状态10(NFA 的终止状态),所以 F={B, C, D}
可以画出 DFA:
python 代码实现:
首先创建 DFA 的数据结构,由于 DFA 是 NFA 的一种特殊情况,所以和前面 NFA 的代码很相似
需要注意的是,DFA 的 trans_table 的类型注解和 NFA 略有不同
class DFA():
def __init__(self) -> None:
self.states: set[int] = set()
self.s0: int = None
self.final: set[int] = set()
self.conditions: set[str] = set()
self.trans_table: dict[int, dict[str, int]] = {}
def __repr__(self) -> str:
return f"S: {self.states}\n∑: {self.conditions}\nM: {self.trans_table}\ns0: {self.s0}\nF: {self.final}"
然后实现辅助函数 epsilon_closure 和 move
class NFA():
def __init__(self) -> None:
...
# 使用记忆化, 空间换时间
self.e_closure_rem: dict[int, set[int]] = {}
...
def epsilon_closure(self, T: set[int]) -> frozenset[int]:
if not T <= self.states:
raise KeyError("some states is not in NFA")
result: set[int] = T
for s in T:
if s in self.e_closure_rem:
result = result.union(self.e_closure_rem[s])
continue
next_states = self.trans_table[s].get(EPSILON)
if next_states:
self.e_closure_rem[s] = self.epsilon_closure(next_states)
result = result.union(self.e_closure_rem[s])
return frozenset(result)
def move(self, T: set[int], a: str) -> set[int]:
if not T <= self.states:
raise KeyError("some states is not in NFA")
if a not in self.conditions:
raise KeyError("no such condition")
result: set[int] = set()
for s in T:
next_states = self.trans_table[s].get(a)
if next_states:
result = result.union(next_states)
return result
最后实现子集构造算法函数 subset_construction
def subset_construction(nfa: NFA) -> DFA:
dfa: DFA = DFA()
Dstates: dict[frozenset[int], int] = {}
unmarked: list[frozenset[int]] = []
dfa.conditions = nfa.conditions - {EPSILON}
s0 = nfa.epsilon_closure({nfa.s0})
dfa.s0 = Dstates[s0] = 0
dfa.trans_table[0] = {}
unmarked.append(s0)
while len(unmarked):
T = unmarked.pop()
for char in dfa.conditions:
U = nfa.epsilon_closure(nfa.move(T, char))
if not U:
continue
if U not in Dstates:
new_state = len(Dstates)
Dstates[U] = new_state
dfa.trans_table[new_state] = {}
unmarked.append(U)
dfa.trans_table[Dstates[T]][char] = Dstates[U]
dfa.states = set(Dstates.values())
for s in Dstates:
if s.isdisjoint(nfa.final):
continue
dfa.final.add(Dstates[s])
return dfa
nfa = Regex("a(b|c)*").to_nfa()
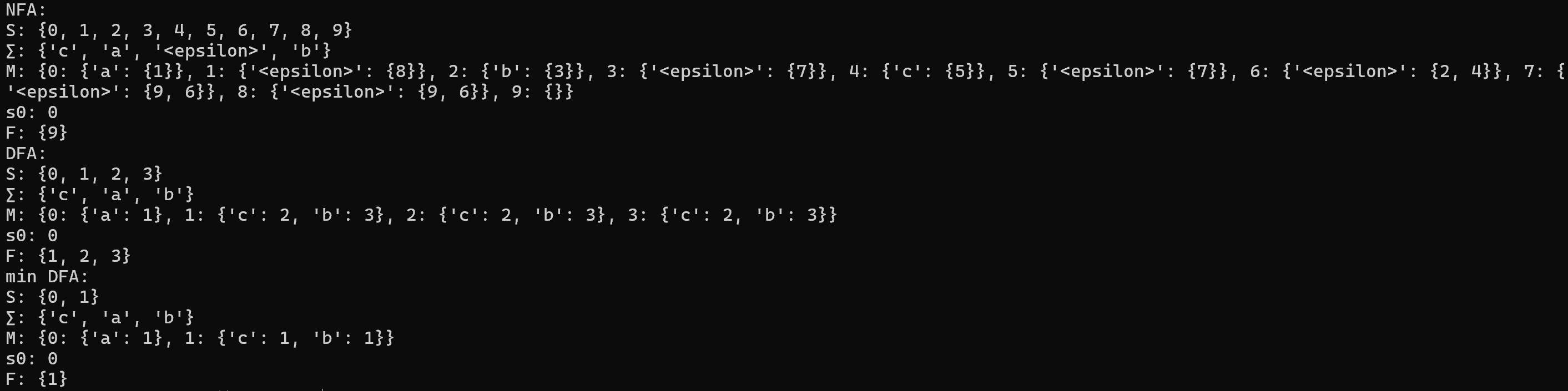
print(f"NFA:\n{nfa}")
print(f"DFA:\n{subset_construction(nfa)}")
hopcroft 算法: 最小化 DFA
虽然我们使用子集构造算法成功将 NFA 转换为了 DFA,但是还不够,我们总是希望 DFA 的状态能够尽量少,因为我们在构造转换函数 M 时需要给每个状态分配条目,每个额外的状态都会带来不小的开销
为了解决这个问题,图灵奖得主 John Edward Hopcroft 发明了 hopcroft 算法,通过状态等价的方式获得一个 DFA 的最小化版本
step1. 该算法首先将给定 DFA 的所有非终止状态 S-F 合并为状态 N,将所有终止状态 F 合并为状态 A,此时称 ∏={N,A} 为初始划分
step2. 对于 ∏ 中的每个分组 G,都尝试将其划分为更小的组;划分规则:状态 s 和 t 在若想要保持在同一个组中,则要求对于所有的 a∈∑,状态 s 和 t 在 a 上的转换都到达 ∏ 中的同一个组
step3. 若 G 可分,则 G 替换为分割后的组,重复 step2,3 直到 ∏ 中所有组都不再可分
伪代码
split(S):
foreach(char in ∑):
if char can split S:
split S into T1, ..., Tn
return T1, ..., Tn
hopcroft(DFA):
split DFA.S into N, A
while(set is still changes):
if (can split(set)):
replace set to T1, ..., Tn
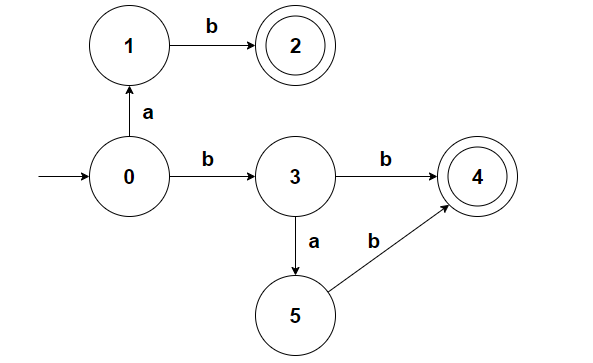
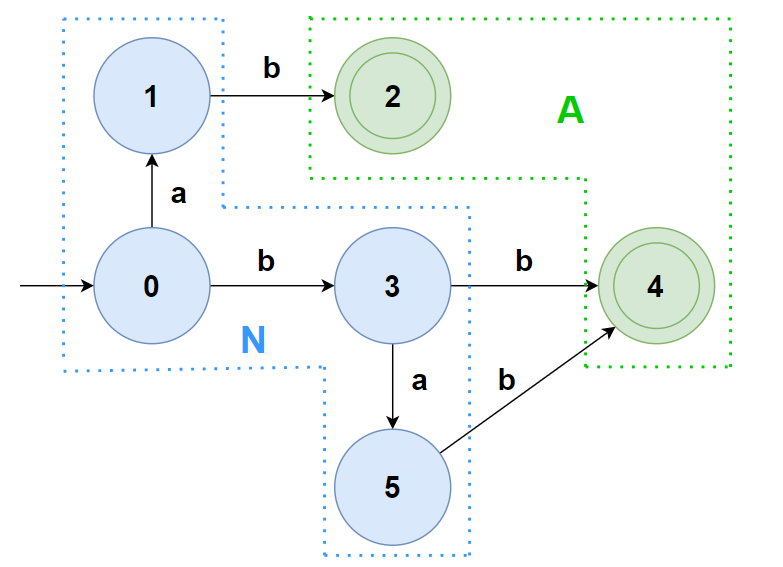
例如对于下面的 DFA,我们尝试使用 hopcroft 算法来减少其状态数:
首先按照是否为终止状态分为 N,A 两组
对于 N 组,看条件 a,可以将其分为 {0, 3} 和 {1, 5}(前者该条件指向 N 组,后者该条件指向 ∅)
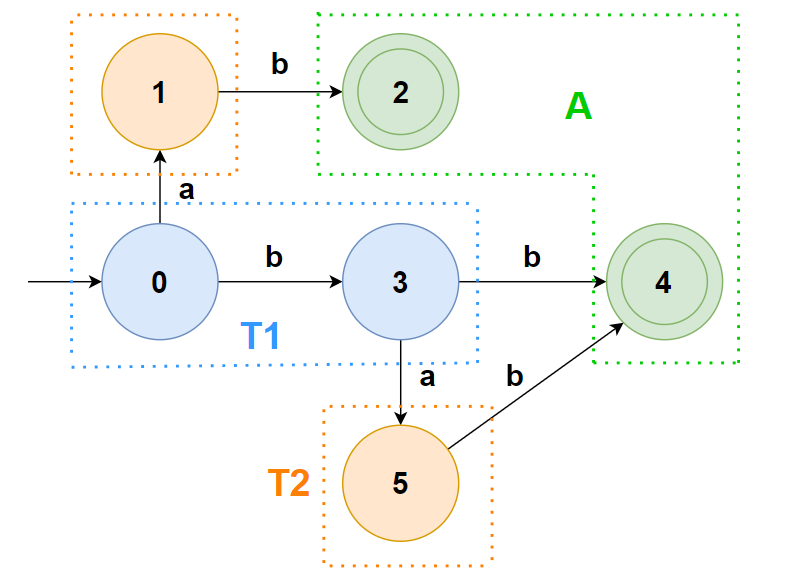
不用再看条件 b,直接分割:
对于 T1 组,看条件 a,都指向了 T2 组;看条件 b,可以将其分割为 {0} 和 {3}(前者该条件指向 T1 组,后者该条件指向 A 组)
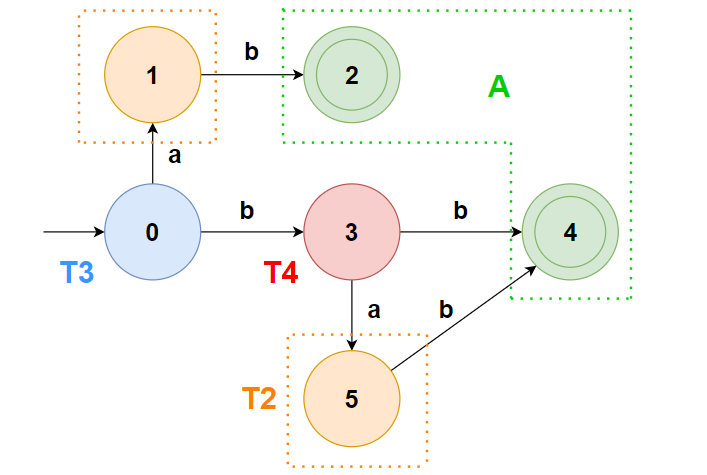
于是有:
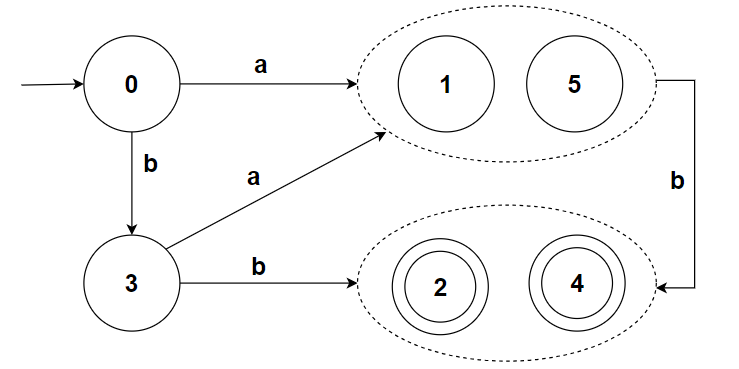
此时无论是哪个组,都无法分割了,于是我们能获得最小化的 DFA 如下:
python 代码实现:
先实现状态的划分
def splite(states: set[frozenset[int]], dfa: DFA, group: frozenset[int]) -> list[frozenset[int]]:
for char in dfa.conditions:
trans_to: dict[frozenset[int], set[int]] = {}
for s in group:
next_s = dfa.trans_table[s].get(char)
if not next_s:
if None not in trans_to: trans_to[None] = set()
trans_to[None].add(s)
continue
for ss in states:
if next_s in ss:
if ss not in trans_to: trans_to[ss] = set()
trans_to[ss].add(s)
break
if len(trans_to)-1:
return [frozenset(i) for i in trans_to.values()]
return [group]
def hopcroft(dfa: DFA) -> DFA:
N: frozenset[int] = frozenset(dfa.states - dfa.final)
A: frozenset[int] = frozenset(dfa.final)
states: set[frozenset[int]] = {N, A}
while True:
for G in states:
splite_g = splite(states, dfa, G)
if len(splite_g)-1:
states.remove(G)
states.update(splite_g)
break
else:
break
...
对于划分好后的状态,每个组随意选择一个状态作代表,然后将组内其他状态的相关的弧转移到代表上
def rebuild_dfa(old_dfa: DFA, state_groups: set[frozenset[int]]) -> DFA:
import copy
dfa: DFA = copy.copy(old_dfa)
Dstates: dict[int, int] = {}
for ss in state_groups:
leader: int = dfa.s0 if dfa.s0 in ss else None
for s in ss:
if leader is None:
leader = s
elif s != leader:
dfa.states.remove(s)
dfa.trans_table[leader].update(dfa.trans_table[s])
del dfa.trans_table[s]
Dstates[s] = leader
for s in dfa.trans_table:
for char in dfa.trans_table[s]:
next_s: int = dfa.trans_table[s][char]
dfa.trans_table[s][char] = Dstates[next_s]
dfa.final &= dfa.states
return dfa
def hopcroft(dfa: DFA) -> DFA:
...
return rebuild_dfa(dfa, states)
nfa = Regex("a(b|c)*").to_nfa()
print(f"NFA:\n{nfa}")
dfa = subset_construction(nfa)
print(f"DFA:\n{dfa}")
min_dfa = hopcroft(dfa)
print(f"min DFA:\n{min_dfa}")
可以看到 a(b|c)* 的最小化 DFA 的状态是非常少的,显著减小了开销
从 DFA 导出词法分析算法
通过前面介绍的算法的处理,我们成功将一个正则表达式转化成了等价的 DFA
此时我们就要用这个 DFA 来做词法分析了
首先我们从单个词法规则入手,构建完成 DFA 后,可以有如下伪代码使得 DFA 能够识别一个词法单元
nextToken()
state = DFA.s0
while (state is not ERROR):
if (state in DFA.F):
return token
eat a char
c = current_char
state = DFA.M[state][c]
return NoMatch
python 实现:
class Lexer():
def __init__(self, input_: str, dfa: DFA) -> None:
self.input: str = input_
self.ptr: int = 0
self.current_char: str = ''
self.dfa: DFA = dfa
def move(self) -> None:
self.ptr += 1
if self.ptr < len(self.input):
self.current_char = self.input[self.ptr]
else:
self.current_char = ''
def next_token(self) -> Token:
state: int = self.dfa.s0
literal: str = ''
while state:
if state in self.dfa.final:
return Token("AToken", literal)
self.move()
c: str = self.current_char
literal += c
state = self.dfa.trans_table[state].get(c)
return Token("NoMatch", literal)
rule: Regex = Regex(r"hello|world")
src = "hello world"
dfa: DFA = subset_construction(rule.to_nfa())
lexer: Lexer = Lexer(input_=src, dfa=dfa)
for _ in range(3):
print(lexer.next_token())
上述代码使用了“最短匹配”的规则,即一旦到达终止状态,则不理会后续字符,直接输出词法单元并回到开始状态
但是,为了不发生下面这样的情况:
对于词法规则
a(b|c)*,输入abc,读入a,进入终止状态,输出[AToken 'a']对于后面的 “bc” 则不符合规则,输出
[NoMatch 'b'] [NoMatch 'c']最终识别结果:
[AToken 'a'] [NoMatch 'b'] [NoMatch 'c'](期望结果应当是[AToken 'abc'])
我们应遵从“最长匹配”原则,即一直尝试读入字符,直到无法找到合法的转移条件,此时回退到上一个匹配的模式并输出
此时我们可以使用一个栈来保存历史状态
class Lexer():
def __init__(self, input_: str, dfa: DFA) -> None:
self.input: str = input_
self.ptr: int = -1
self.dfa: DFA = dfa
@property
def current_char(self) -> str:
return self.input[self.ptr] if self.ptr < len(self.input) else ''
def move(self) -> None:
self.ptr += 1
def rollback(self) -> None:
self.ptr -= 1
def next_token(self) -> Token:
state: int = self.dfa.s0
literal: str = ''
state_stack: list[int] = []
while state is not None:
state_stack.append(state)
self.move()
c: str = self.current_char
literal += c
state = self.dfa.trans_table[state].get(c)
while len(state_stack):
state = state_stack.pop()
self.rollback()
if state in self.dfa.final:
break
literal = literal[:len(state_stack)]
if state in self.dfa.final:
return Token("Token", literal)
self.move()
literal += self.current_char
if literal:
return Token("NoMatch", literal)
return Token("EOF", '')
rule: Regex = Regex(r"a(b|c)*")
src = input("please enter your code: ")
dfa: DFA = subset_construction(rule.to_nfa())
lexer: Lexer = Lexer(input_=src, dfa=dfa)
while True:
token = lexer.next_token()
if token.type == "EOF":
break
print(token, end=' ')
print('')
对于多个需要并行分析的词法规则,例如:
运算符:
+|-|\*|/|=|==|>|<关键字:
if|else|return|true|false整数:
(1|2|3|4|5|6|7|8|9)(0|1|2|3|4|5|6|7|8|9)*
我们对每个词法规则单独构建 NFA:N1、N2… Nk,然后创建一个新的 NFA 状态 s 作为词法分析器的起始状态,然后用 ε 条件连接 s 和 N1-Nk 的起始状态,最后将这个新的 NFA 转换为 DFA
需要注意的是,如果我们想要实现类似 Lex 的 [每个词法规则匹配一个“动作”] 的功能
// 该例子来自龙书
a {模式 p1 的动作 A1}
abb {模式 p2 的动作 A2}
a*bb* {模式 p3 的动作 A3}
那在 NFA 转换 DFA 的时候就要注意将每个终止状态和其对应的匹配规则联系起来
可是正如上面的例子那样,部分规则是有“交集”的,例如当我们匹配到 “abb” 时,可能是命中了模式 abb,也可能是命中了模式 a*bb*
为了避免混乱,通常来讲一个终止状态只能匹配一个确定的动作;一般来说遵从以下原则:先出现的模式优先级更高
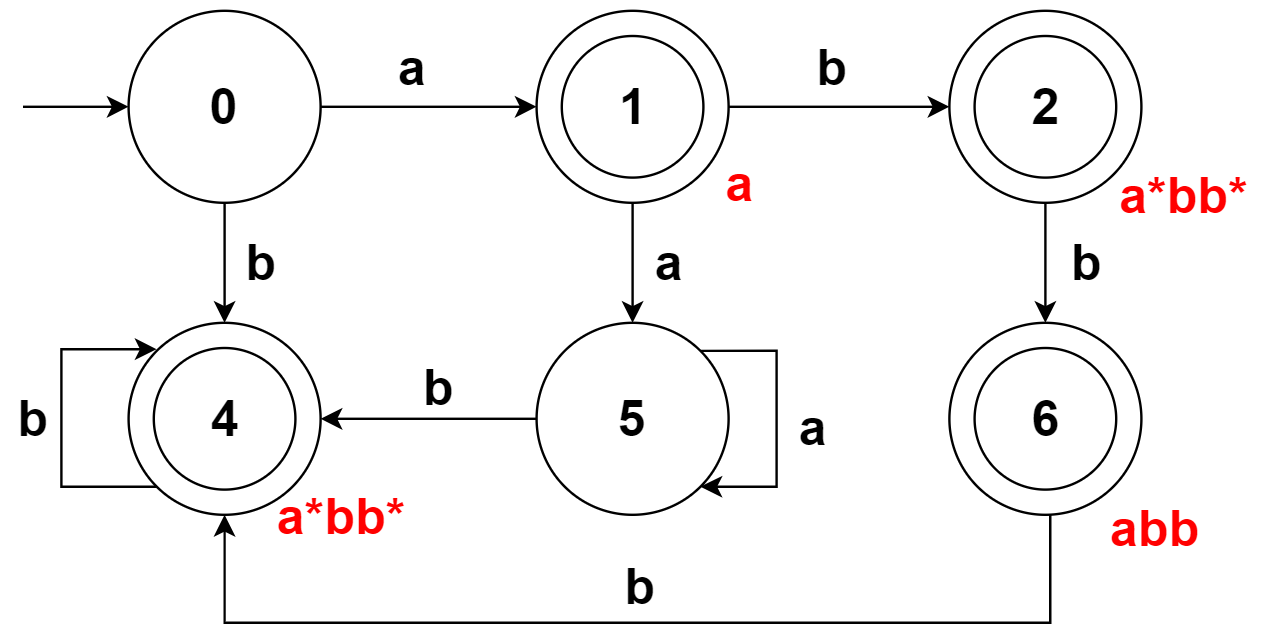
以上述规则为例,能构造出 DFA:
对于可能产生歧义的状态 6,由于用户输入中,先规定了模式 abb 再规定模式 a*bb*,所以 abb 优先级更高,也就成为状态 6 关联的模式
之后使用“最长匹配”的驱动代码运行该 DFA 即可,至此词法分析专题结束
附录
一个手工构造的词法分析器的完整示例,目标是解析下面的词法规则
| 词法单元 | 规则(使用 regex 表示,会包含部分语法糖) |
|---|---|
| 标识符 | [a-zA-Z_][a-zA-Z0-9_]* |
| 关键字 | if|else|return|true|false|func |
| 运算符 | \+|-|\*|/|=|==|>|< |
| 数字 | \d+ |
| 分隔符 | \(|\)|\[|]|{|}|; |
token.py
from enum import StrEnum, auto
class Token():
def __init__(self, type_: str, literal: str = '') -> None:
self.type: str = type_
self.literal: str = literal
def __repr__(self) -> str:
return f"[{self.type} '{self.literal}']"
class TokenType(StrEnum):
EOF = auto()
ILLEGAL = auto()
WHITESPACE = auto()
IDENTIFIER = auto()
KEYWORD = auto()
OPERATOR = auto()
NUMBER = auto()
SEPARATOR = auto()
keywords: set[str] = {"if", "else", "return", "true", "false", "func"}
lexer.py
from token import Token, TokenType, keywords
def is_letter(char: str) -> bool:
return ('a' <= char and char <= 'z') or ('A' <= char and char <= 'Z') or char == '_'
def is_digit(char: str) -> bool:
return char >= '0' and char <= '9'
class Lexer():
def __init__(self, input_: str) -> None:
self.input: str = input_
self.ptr: int = 0
@property
def current_char(self) -> str:
return self.input[self.ptr] if self.ptr < len(self.input) else ''
@property
def peek_char(self) -> str:
ptr: int = self.ptr + 1
return self.input[ptr] if ptr < len(self.input) else ''
def move(self) -> None:
self.ptr += 1
def read_idertifier(self) -> str:
literal: str = ''
char: str = self.current_char
while is_letter(char) or is_digit(char):
literal += char
self.move()
char = self.current_char
return literal
def read_number(self) -> str:
literal: str = ''
char: str = self.current_char
while is_digit(char):
literal += char
self.move()
char = self.current_char
return literal
def read_whitespace(self) -> str:
literal: str = ''
char: str = self.current_char
while char.isspace():
literal += char
self.move()
char = self.current_char
return literal
def next_token(self) -> Token:
token: Token = Token(TokenType.EOF)
if not self.current_char:
return token
match self.current_char:
case '+': token = Token(TokenType.OPERATOR, '+')
case '-': token = Token(TokenType.OPERATOR, '-')
case '*': token = Token(TokenType.OPERATOR, '*')
case '/': token = Token(TokenType.OPERATOR, '/')
case '=':
token.type = TokenType.OPERATOR
if self.peek_char == '=':
self.move()
token.literal = '=='
else:
token.literal = '='
case '>': token = Token(TokenType.OPERATOR, '>')
case '<': token = Token(TokenType.OPERATOR, '<')
case '(': token = Token(TokenType.SEPARATOR, '(')
case ')': token = Token(TokenType.SEPARATOR, ')')
case '[': token = Token(TokenType.SEPARATOR, '[')
case ']': token = Token(TokenType.SEPARATOR, ']')
case '{': token = Token(TokenType.SEPARATOR, '{')
case '}': token = Token(TokenType.SEPARATOR, '}')
case ';': token = Token(TokenType.SEPARATOR, ';')
case _:
if self.current_char.isspace():
token.type = TokenType.WHITESPACE
token.literal = self.read_whitespace()
return token
elif is_letter(self.current_char):
token.literal = self.read_idertifier()
if token.literal in keywords:
token.type = TokenType.KEYWORD
else:
token.type = TokenType.IDENTIFIER
return token
elif is_digit(self.current_char):
token.type = TokenType.NUMBER
token.literal = self.read_number()
return token
else:
token.type = TokenType.ILLEGAL
token.literal = self.current_char
self.move()
return token
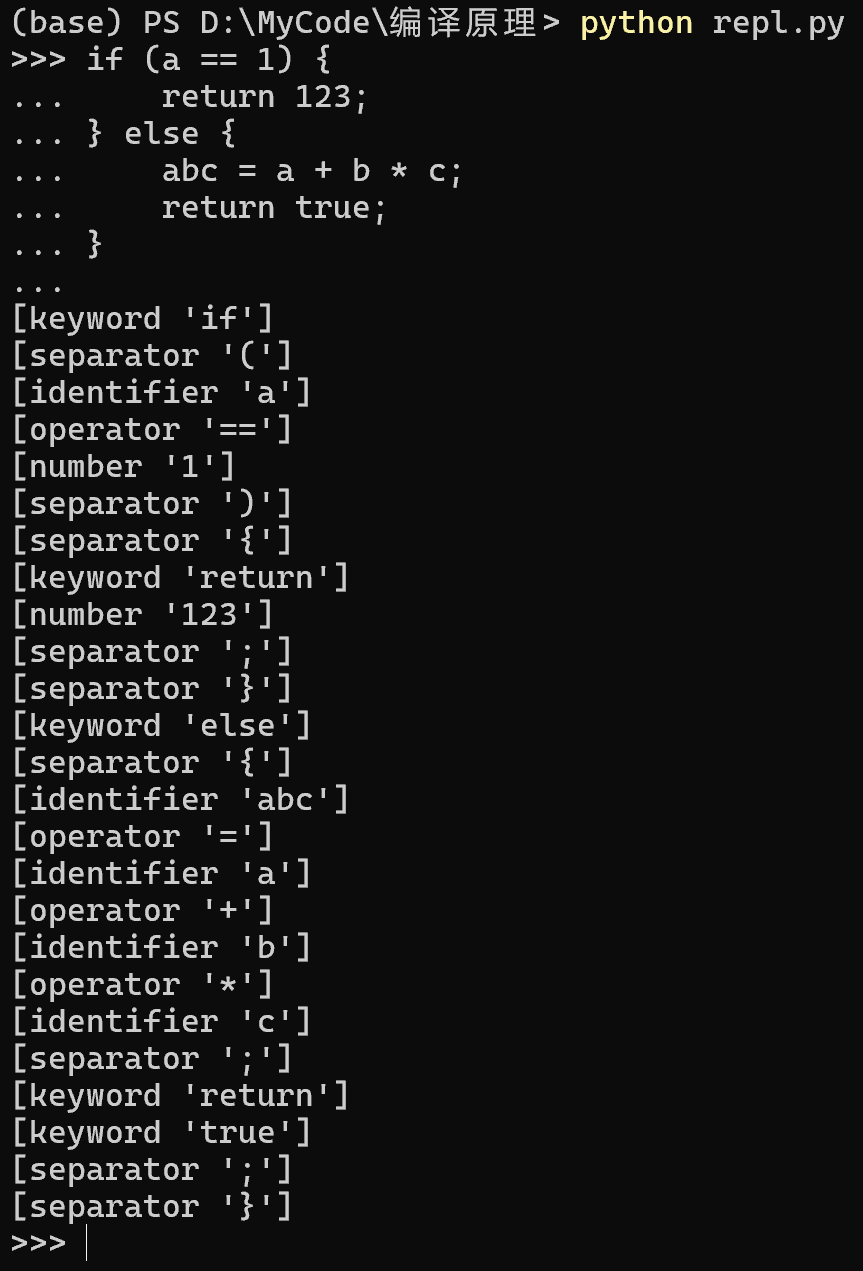
repl.py(read-eval-print loop)
from token import Token, TokenType
from lexer import Lexer
def _read() -> str:
result: str = input(">>> ")
while result:
code = input("... ")
if not code:
break
result += '\n' + code
return result
def _eval(code: str) -> list[Token]:
if not code:
return []
result: list[Token] = []
lexer: Lexer = Lexer(code)
while True:
token: Token = lexer.next_token()
if token.type == TokenType.EOF:
break
result.append(token)
return result
def _print(tokens: list[Token]) -> None:
for token in tokens:
if token.type == TokenType.WHITESPACE:
continue
print(token)
if __name__ == "__main__":
while True:
_print(_eval(_read()))